课时二刷提升 $2$ 讲解

课时二刷提升 $2$ 讲解

这个我会！不就是求 $\begin{cases}x<0 \\y>0 \\y \geq 2x+6\end{cases}$ 有多少整数解吗？

那我直接枚举 $x$，看对应的 $y$ 有多少不就行了吗？

哇，和答案想的竟然一摸一样！我真是个天才！

课时二刷提升 $2$ 讲解

结束了？

如果你是出题人，你会怎么出这道题？

课时二刷提升 $2$ 讲解

结束了？

如果你是出题人，你会怎么出这道题？

要是不等式的数量变多，你是否还会选择枚举法求解？

课时二刷提升 $2$ 讲解

我们考虑换一种方式刻画答案。

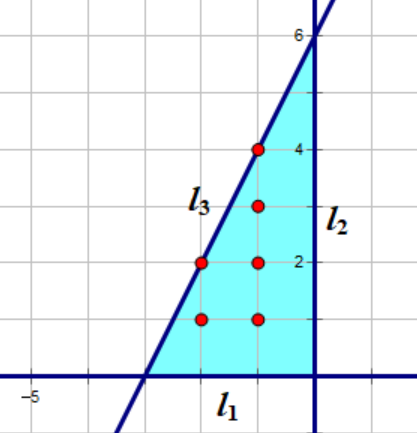
于是这道题就会更加优美简单。

课时二刷提升 $6(3)$ 讲解

课时二刷提升 $6(3)$ 讲解

原题很简单。

课时二刷提升 $6(3)$ 讲解

原题很简单。

经过计算可知，当 $P$ 到达 $C$ 时，$Q$ 的坐标为 $(2,6)$。而 $P$ 到达 $B$ 时，$Q$ 的坐标为 $(7,6)$。

所以，这段过程中 $S_{\delta APQ}=\dfrac{PQ \times AB}{2}$，可得 $PQ=1$。此时讨论 $P$ 与 $Q$ 的位置关系或者大力解绝对值方程即可。

答案为 $t=4.5$ 或 $t=5.5$。

课时二刷提升 $6(3)$ 讲解

结束了？

如果你是出题人，你会怎么出这道题？

课时二刷提升 $6(3)$ 讲解

结束了？

如果你是出题人，你会怎么出这道题？

比如，在 $P$ 到达 $C$ 时，$Q$ 如果还没有到达 $C$，又是另一个故事。

或者，运动时间很长，分类讨论很繁琐，这又是另一个故事。